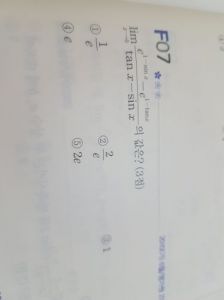>>67
>たまたま簡単になって
(e^y-1)/y の形に持ち込めたに過ぎない。
そもそもそういう出題なのではありませんか?
つまり、問題文の数式を見て(e^y-1)/y の形を想起できるかどうかを試している問題だと思います。
「たまたま簡単になる」解法がバカにされる所以はありません。そもそも高校生(大学初年級)レベルの問題なんて、出題者が「たまたま解ける問題」を選んで出題しているのではありませんか?
あなたの主張は、たまたま因数分解できる方程式を無理やり解の公式を用いて解いて「こちらの解き方が汎用性がある。その解き方はたまたま因数分解できただけだ」言っているように見えます。
>このy->0 における極限が1になることの根拠をチョンの解答は示せていない。
これは「eの定義」と言ってもよい事項であり、根拠を示す必要があることではないと思いますが。>>70
数学は将棋みたいなものと言った。
大半の人は棋士にはなれない。しかし、将棋を指して楽しんでいる。将棋を楽しめば、こうすればこうなると言った思考方法が自然と身につく。我々凡人が数学を勉強するのは、これと同じで論理的思考の鍛錬の為なのだ。論理的思考の鍛錬を十分やると合格率が下がるからと進学校ではあまりやらないのではないかな。
チョンがすっ飛ばした
lim_y->0 (e^x-1)/x =1
を高校生にどのように理解させれば良いかは、大学卒レベルの基礎学力がある人なら考えるに値する良い問題になろう。部下をどのように教育すれば良いかは管理職にとって重要な問題なのだから。>>72
極限を題材にして、たまたまそうなるのを見つける能力を要求するのは、全くもってくだらないと私は考えています。世の中はたまたまそうなるものはごくわずか。そもそも貴方が仰る指数関数の定義にしても、高校生が理解するのは無理ですよ。a^xにしても高校生が理解できるのはxが有理数(分数で表すことができる数)の場合だけで、いきなりxが実数の場合にまで拡張するのは論理的飛躍があるのではありませんか?ある著名な数学の大家が高校生の時にその飛躍に全く気がつかなかったと述懐しているのを学生の頃に見つけ、私も恥じ入ったことを思い出しました。まあ、その辺りはいい加減にして、チョンがすっ飛ばしたlim_y->0 (e^x-1)/x =1
を高校生でも分かるように説明してみましょう。e^xの導関数あるいは原始関数はe^x, e^0=1位は前提にしましょうか。
まずグラフを描いて0<x<<1の範囲で
1+x<e^x<1+2x
を納得させますね。
e^xの原始関数はe^xですから
e^x=区間(0,1)におけるe^xの定積分+1
くらいは高校生でも分かるでしょう。
これに先程の不等式を利用すれば
x+x^2/2<e^x-1<x+x^2
だから
1+x/2<(e^x-1)/x<1+x
ここで、xをどんどん小さくすると
(e^x-1)/xの範囲は1に限りなく近く。
これを(e^x-1)/xのx->0における極限としましょうとするのです。つまり
lim_y->0 (e^x-1)/x = 1.
勿論、この説明はあくまで高校生向けで、きちんとした説明は実数の連続性あたりのごちゃごちゃした循環論法に寄らなければなりません。今の大学でここら辺りをちゃんと教えてるのでしょうかね?定義より明らかという御呪いには若い頃の私はかなり反発しましたが、今の若い人は従順ですねー。www
反射神経的計算で満足していると、チョンと変わりませんよ。しっかりしましょう。>>75
>極限を題材にして、たまたまそうなるのを見つける能力を要求するのは、全くもってくだらないと私は考えています。
あなたがくだらないと考えるのは自由ですが、私はくだらないとは思いません。
そういう能力はいろいろな場面で重要になると思います。
例えば純粋に数学という学問を追い求めている人と数学を単なる道具として使っている人では、どこまで論理性を追求すべきかは異なってくるのではありませんか?
「自分がそう考える」ことを根拠として、「他者が自分と同じように考えない」ことをバカにするのは間違っているのではありませんか?
>そもそも貴方が仰る指数関数の定義にしても、高校生が理解するのは無理ですよ。
だからこの問題の解法を説明する場合に「lim_y->0 (e^x-1)/x =1」の根拠を説明する必要は無いのではありませんか?
>e^xの導関数あるいは原始関数はe^x, e^0=1位は前提にしましょうか。
あなたもお気づきだと思いますが、あなたの説明は「循環論法」になっています。>>74
AIを使うとアガシはよがりまくりますねー。w
Amazon USAで日立のMagic Wand Massagerのカスタマーレビューの点数が5点満点で4.6です。世界の女性とそのパートナーを幸せにする為に貢献していますよ。>>1
ハングルを読もうと思わんので
そら解けんわな- 82
名無し2018/02/01(Thu) 13:24:40(1/1)
このレスは削除されています
めちゃ簡単、9センチ
>>80
日本の恥をさらしていることに気づきましょう。>>76
昼飯食いながら読み直したら、確かに循環してたよ。
e^xの微分はe^xとe^0=1を微分係数の定義に掘り込めば
lim_x->0 (e^x-1)/x =e^0=1
だな。年は取りたくないね〜。
すると、今度は対数函数の連続性を言わなきゃならなくなるな。
そうすると、先に触れた指数関数の連続性、逆函数の連続性まで必要になる。高校では有理数の実数における稠密性、連続性あたりを誤魔化して教えてるんだな。これを認めると、
e^x=1+1/sと置いて、x=log(1+1/s)という技巧的な形を使って、
(e^x-1)/x=1/s log(1+1/s)=1/log (1+1/s)^s
x->0 ならs->無限大(めんどくさいから一応+無限大にしとく)
これで説明するってことか。>>1
宿題をこんなところで訊くんじゃないよ。>>63 별 좆도아닌 고교문제에 응용력이니 기초능력이니 하고있어 니가 못푸는건 그냥 니가 멍청해서 모르니가 못푸는거야
4점 킬러 문제도 아니고 3점의 거저 주는 문제에 발광하는
일본인한국에서 시험칠때 이런 문제는 2분 안에는 풀어야 된다
>>91
おお、これこそチョンの精神的勝利だ。優しい問題を素早く解く。
頑張ってねwww。韓国ではおそらく数学が好きな学生さんは少ないだろうね。じっくり納得行くまで考えて到達する喜びと言うのは、韓国の教育では涵養されないだろう。入試問題にストーリー性がない。ただの知能検査と同じだ。私は旧帝大の入試、6問150分くらい、の形式ですら不十分だと思っているから、韓国の入試問題はただただ笑ってしまう。
>>51
한국인이 논쟁에서 열세 있다고 보여지는 것은 인수분해가 통하지 않는 문제라면 그런 문제의 해법도 터득해야 하기 때문에 공부하고 또 공부해야 하는 것이다. 이것이 한국 고등학교 교육의 비극인 것이야.韓国の数学教育では論理的思考が育たない。慰安婦合意に対し破棄や再交渉はしないが日本は自発的に謝罪しろと言う韓国政府の非論理性がそれを端的に示している。ダメだコリア。
>>95
이런 곳에서까지 억지로 정치 문제를 거론하다니..
이것도 병이다. www
하긴 5-60대 할아버지에게 무슨 말이 통하겠냐만은.. ㅎㅎ누가 이 병신한테 4점 문제 보여줘라 www
韓国に論理性を感じないのは、日本人だけではない。その理由の一端として韓国の数学教育が挙げられる。
私はこのスレを通して、韓国の大学入試の問題を眺め、詰め込み、丸暗記と言う印象をうけたが、韓国でもそれを指摘する声があるようだ。
http://m.hani.co.kr/arti/society/schooling/693383.html#cb겨우 3점의 계산 문제로 교육을 평가하는 병신 ww
그것도 자기가 했던 풀이는 고등학교 과정에서 다루지도 않으면서
계산식만 많은 쓰레기 풀이였다 wwww>>100
평범한 4점의 문제입니다 ^ ^이제 풀지도 못하고 도망갈 일만 남았네 www
힘내라 ^ ^일본 고등학생 수학 문제도 내보면?
바보 일본인은 문제 접근도 못하는 소리가 들리죠 www
チョンの精神的勝利だな。
>>108
네 다음 고도의 사고력 응용력 개념에 대한 확실한 이해가 없으면 풀지 못하는 4점의 문제는
건드리지도 못하는 일본인 wwwwwwwwww2,3점 문제는 대충 이 사람이 그래도 수업 시간에 책은 폈을까? 정도의 간단하고 4점을 풀 정도의 기본적인 소양은 있는가?를 물어봅니다
변별력은 4점에서 나옵니다>>112
日本人からしたら、韓国人の知能テストに協力する義理がない。どうしても回答して欲しいのなら、礼儀を尽くして頼むか、お前が報酬を出すとかしたらどうだ? そうすれば誰か参加してくれるかもしれないぞ。ちなみに、自分は分からないからパス。g(t)の定義式の積分範囲を(k,k+7.2347)に変更したら、どんな等式が得られるんだ?それに答えられたら、答えてやるよwww。
2,3점 문제 이 정도는 간단한 DESU~
한국인은 BAKA DESU~
4점 -> 도망 wwwwwwwww
일본 입시 문제도 한번 내보세요공학 수학을 내고 있네 고등학생한테 미친 새끼 www
7.2347이란다 병신이
문제식만 더럽게 복잡하게 만들라고
3939020x2039383922020 암산해라
계산기 없이 같은 개소리チョンの精神的勝利だな。
難しい問題ならいくらでも作れるぞ。
数学オリンピックの問題を出せばいいだけだ。問題はそれで選別できるのは、全国で数人くらいということ。
つまり実質的にそんな問題は無意味になるってことだよ。チョンはそれが理解できずに、韓国の問題はこんなに難しいだろう、参ったか、チョッパリと言いたいんだよ。精神年齢は小学生だな。ちなみにノーベル物理学賞もらった人でも大学入試に失敗してるんだよ。
韓国にいたら、そんな人は失業者だなwww。微積の問題かな?懐かしい。
日本人に威張ったところで、自慢にはならないな。
羅老ロケットの2度の失敗原因。ロケットの突入角度、分離時間、2段目ロケットの燃焼開始時間…等。
これらの問題は、韓国人に微積の高度な計算が出来ていたのかは、疑わしいぞ。
(1)小型の実験ロケットの作成
↓
(2)実験ロケットを改良して成層圏などを観測する観測ロケットの作成
↓
(3)観測ロケットを改良して大気圏の外を飛ぶ準軌道ロケットの作成
↓
(4)準軌道ロケットを改良して衛星を周回軌道に乗せる事ができる打ち上げロケットの作成
普通なら、こういう段階を経て衛星打ち上げをやるんだが、韓国は(1)~(3)の技術的蓄積を省略して(4)からやろうとした。
それに加えて、衛星軌道に人工衛星を乗せる為に必要な速度を満たす為のロケット分離技術。
その技術的な未熟性を誤魔化す為に、3段~4段ロケットにするところを、2段ロケットでやろうとしている。
この点からも、韓国のロケット開発には、技術的な問題と、それに合わせた微積計算が出来てるのかは疑わしい。
省略して(4)から始めるという韓国のロケット開発の未熟な技術蓄積に対して、失敗の原因をロシアのせいにするのは根本的に間違いだ。
道路標識の知識すら疑わしい&車の運転が出来るようになる段階を経てない無免許運転の者が、衝突事故を起こした後に、
「俺の運転に一切の問題はなく、ロシア製の車の故障が原因だった」と言われても、誰も信用しないのと同じだ。
이거 풀수있는 사람있냐??
120
ツイートLINEお気に入り 67
67 50
50