일본의 수학교재

1ㅇㅇ2016/12/05(Mon) 12:20:43ID:UwNjExNzU(1/7)NG報告
한국의 수능(일본의 센터시험과 유사) 수학 문제는 일본의 수학문제를 베껴서 냅니다.
그래서 일본의 수학교재에 대해 알고 싶습니다.
>>8 >>17 >>18 >>19
2ㅇㅇ2016/12/05(Mon) 16:23:31ID:UwNjExNzU(2/7)NG報告
문제의 내용은 "정육면체를 자른 단면에 대한 것 중 올바른 것으로 짝지어진 것을 고르시오."입니다.

출저:立体のとらえかた (発見的教授法による数学シリーズ5) 1989년 출간
3ㅇㅇ2016/12/05(Mon) 16:25:11ID:UwNjExNzU(3/7)NG報告
94학년도 2차 수능 수학의 문제입니다.
문제의 내용은 "정육면체를 자른 단면의 모양은 <보기>중 몇가지가 되는가?"입니다.
당시 정답률 4% 였습니다.
>>13
4DinoSwift2016/12/05(Mon) 16:26:40ID:gyNzk2NTA(1/1)NG報告
画像がハングルで書かれていて翻訳されてないので何が書いてあるかさっぱり分からん　ｗ
5名無し2016/12/05(Mon) 16:42:42ID:A5NTYyMzU(1/3)NG報告
<表示>の内容を訳してくれ、いや、書き出してくれたら翻訳される。
6名無し2016/12/05(Mon) 16:43:47ID:A5NTYyMzU(2/3)NG報告
そして、翻訳されるまでも無く正解率4％とか問題がおかしい予感しかしない。
7名無し2016/12/05(Mon) 16:49:34ID:A2ODY3MzA(1/1)NG報告
日本のセンター試験は、韓国の修学能力試験のように、絶対的なものではありません。
下の図は東大の入試のセンター試験と二次試験の配点の配分比率です。
左の列はセンター試験で、配点の合計の９００点を、１１０点に変換します。
そして、右の列は大学独自で行う二次試験の配点の４４０点です。
東大の試験は、センター試験と二次試験の合計点数５５０点で、評価されます。

日本のセンター試験は、一定の学力基準を計るものなので、難問や奇問があまり出ない、素直な問題が多いです。
8名無し2016/12/05(Mon) 17:12:15ID:cxOTc3MjA(1/1)NG報告
>>1
まさかとは思うが韓国の韓国の修学能力試験（日本のセンター試験と同様）数学の問題は、日本のセンター試験を参考に作ってるとか無いよね？
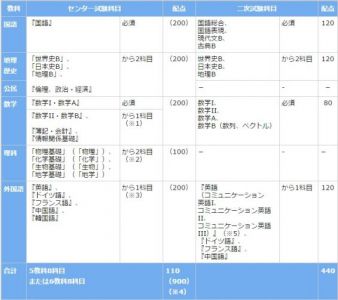
日本の歴代のセンター試験内容は必修とかじゃないんだよね？
9ㅇㅇ2016/12/05(Mon) 17:21:20ID:UwNjExNzU(4/7)NG報告
다음의 (1)-(7) 은 정육면체를 펑면 P로 자른 단면도인 도형 F에 대하여 기술한 것이다. 참인 명제의 기호의 조합을 아래 가~자 중에서 선택하라.
(1) F 가 둔각삼각형으로 되지는 않는다.
(2) F 가 사각형이라면 사다리꼴이 된다.
(3) P 가 정육면체의 꼭지점 중 한개를 포함하면 F 의 꼭지점 개수는 홀수개이다.
(4) P 의 위치를 적당히 정하면 F는 선대칭인 오각형이 된다.
(5) P 의 위치를 적당히 정하면 F는 칠각형이 된다.
(6) 삼각형이 되는 F 중 넓이가 최대인 것은 정삼각형이다.
(7) 직시각형이 되는 F 중 넓이가 최대인 것은 정사각형이다.
가. (1)·(3)·(7) 나 . (2)·(5)·(7) 다. (3)·(4)·(6)
라. (1)·(2)·(3)·(5) 마. (1)·(2)·(4)·(6) 바. (1)·(4)·(5)·(6)
시 . (2)·(3)·(4)·(7) 아. (3)·(5)·(6)·(7)
자. (가)에서 (아)까지 어느것도 아니다.
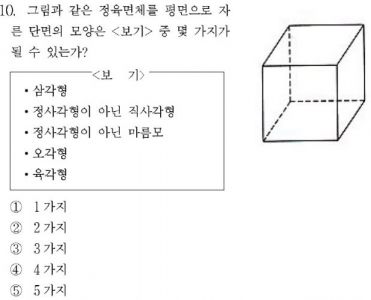
출저:立体のとらえかた (発見的教授法による数学シリーズ5) 1989년 출간
10ㅇㅇ2016/12/05(Mon) 17:24:43ID:UwNjExNzU(5/7)NG報告
10. 그림과 같은 정육면체를 평면으로 자른 단면의 모양은 <보기> 중 몇 가지가 될 수 있는가?
<보기>
·삼각형
·정사각형이 아닌 직사각형
·정사각형이 아닌 마름모
·오각형
·육각형
①1가지
②2가지
③3가지
④4가지
⑤5가지

94학년도 2차 수능 수학의 문제입니다.
>>15
11名無し2016/12/05(Mon) 17:38:34ID:A5NTYyMzU(3/3)NG報告
どれでもないを選ぶのは勇気が必要・・・
12名無し2016/12/05(Mon) 18:01:16ID:Y0MDk0NjA(1/1)NG報告
正答率４％の問題とかよく出せるなｗ
13나그네2016/12/05(Mon) 18:11:18ID:Q4MTY1NzA(1/1)NG報告
>>3
5번?
1412016/12/05(Mon) 19:28:15ID:g1NjMzOTU(1/1)NG報告
한국의 수능 수학문제가 일본을 베껴서 낸다고 ?
아무 근거없는 이상한 소리하고있네
15名無し2016/12/05(Mon) 20:45:28ID:k2NzQ4MDU(1/1)NG報告
>>10
三角形　可能
長方形　可能
菱形　　可能
正五角形ではない、五角形　なら　可能
六角形、正六角形　も　可能

よって　答えは　⑤　

中学受験（小学生）のレベル
>>21
16ゴンバニ2016/12/06(Tue) 00:01:42ID:g3ODQxMzY(1/1)NG報告
본고사 시절이냐?www
17fff2016/12/06(Tue) 00:03:49ID:gwMDczMzg(1/6)NG報告
>>1

제발 근거를 가지고 말해라.

일본의 센터시험이랑 한국의 수능시험은 난이도 자체가 다르다.
18fff2016/12/06(Tue) 00:05:40ID:gwMDczMzg(2/6)NG報告
>>1

만약 베꼈다면 일본의 본고사를 베꼈겠지.
19fff2016/12/06(Tue) 00:09:59ID:gwMDczMzg(3/6)NG報告
>>1

그리고 요즘 한국의 수능유형은 일본 본고사 유형이랑 많이 다르다.
20名無し2016/12/06(Tue) 00:21:24ID:Q5NTQ2OTA(1/1)NG報告
このまえ上がってた小4の問題は難しかったな…
質問してた韓国人は子供に上手く説明出来たのだろうか…
21fff2016/12/06(Tue) 00:22:06ID:gwMDczMzg(4/6)NG報告
>>15

http://cafe.naver.com/spielmathe/7563

찾아보니깐 초등학교 競試大會對備 및 英才敎育院對備 문제였다 ㅋㅋㅋㅋㅋㅋㅋㅋㅋ

초등학교 문제라는 말도 틀린 말은 아니었다.
>>22
22fff2016/12/06(Tue) 00:23:27ID:gwMDczMzg(5/6)NG報告
>>21

http://cafe.naver.com/spielmathe/7563

찾아보니깐 초등학교 競試大會對備 및 英才敎育院對備 문제였다 ㅋㅋㅋㅋㅋㅋㅋㅋㅋ초등학교 문제라는 말도 틀린 말은 아니었다.

번역 error가 떠서 다시 적습니다.
23ㅇㅇ2016/12/08(Thu) 00:30:24ID:A2MTY2ODA(6/7)NG報告
최근의 예를 가져왔습니다.
일본 분들은 http://server-test.net/math/php.php?name=tokyo&v1=1&v2=1991&v3=1&v4=6&y=1991&n=6 이것을 참조해 주십시오.
>>24
24fff2016/12/09(Fri) 02:33:32ID:QxOTcyMDc(6/6)NG報告
>>23

살짝 다른 것 같네. 물론 풀이는 모르기 때문에 풀이를 봐야지 정확히 알 수 있겠지만.
25名無し2017/01/25(Wed) 09:35:48ID:M0MjkzNzU(7/7)NG報告
제 나름대로 일본의 대입 수험서를 알아본 결과,
総合問題集　最高峰の数学へチャレンジ　（駿台受験シリーズ）
라는 책이 제일 수준이 높은 거 같습니다.
혹시 알고 있는 일본 분 계신가요?