内閣の和すら怪しいからな。
使わな過ぎてサッパリだ。
実を言えば、足し算すら今では怪しい。小学生でこれは難しいですね…
テストのことを考えると補助線の引き方のパリエーションを色々覚えるのが良いのでしょうか>>71
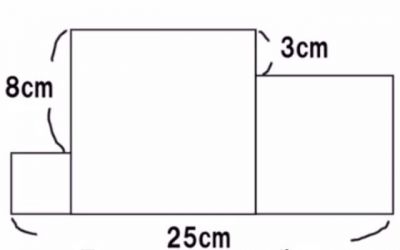
ん！何だこりゃ。200平方センチメートル？
これでいいや。是はそんなに単純ではなさそうだな。
中で殺人事件が起きていて、使える面積が狭いと予想。
単位がセンチメートルなのに、人が入ると言うことは、超小型人類である、古代ミクロ人の可能性がたかい。
そんな狭い領域なら、死体があればすぐに見つかり、犯人も近くに居るだろう。
新たな殺人を危惧した人類は、一番小さい枠の中でしか暮らせなくなるはずだ。
25平方センチメートルが正解か！>>55
高校？小学校の間違いですよね。>>74
ナンプレっぽい解き方ですねいや待てよ、強欲な殺人犯は殺人できなくなる事に不満を募らせるだろう。
一気に爆発した殺人犯の衝動は、止まる事をしらず、その領域にいる人を全て殺害してしまうだろう。
正解の正解は、ゼロだ！>>77の「÷3」って言うのがポイントですな
40 - 32 / 2 = ?
小学生「4!」
理系「よくわかってんじゃん」
文系「やっぱわかんないか～ｗ」>>81
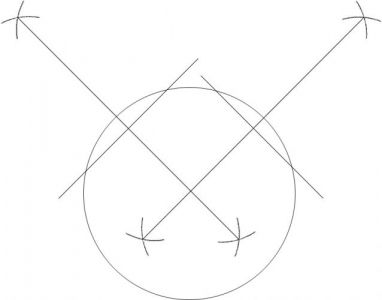
ダーツで正確に射抜く！実は、是にも罠が仕掛けられている！
貴方が見ている円は数年前のもので、今は存在しない！
存在しないものの中心を当てるなど不可能だ！- 86
名無し2016/11/07(Mon) 15:18:12(22/23)
このレスは削除されています
>>55
영어가 없어도 살 수 있는 나라는 뭔가 다르군요!>>82
wwwwwww>>84
（コンパス4 定規2）を、２回ですね。30分以上経過したので、適当な作図ですが、解答を載せておきます。
実は、コンパスを使った円の描き方と、垂直二等分線の引き方が分かる、小学校四年生ならば解ける、ちょっとした応用問題なのですね。>>91
定規の使い方を習った、1年生でも解けるやり方ですねｗ
中学受験算数だと、不正解になりますけれど…。原始時代に定規やコンパス等無い。
結局、誰かが作ったものの引用に過ぎない。
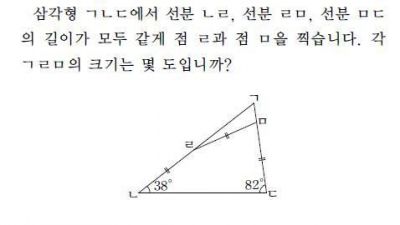
この問題自体が不適切で、不快だ。あれ？30度にならない？
角度ㄹㅁㄴをaと置くと
三角形ㄷㄹㄱの内角の和180は
120+4a になるから
a=15
ㄹは2aだから30。>>65
ちょい待て、めちゃ正解ぽく書いてるが、
> 240=◯＋●＋82+（180-●-●）
この82はどこから出てきた？
「360 - 82 - 38 = ○ + ● + □」の「□」を(180 - ● - ●)に置き換えた式だよね？
> ●=22+◯…ア
あとこれ意味不明。
「● = ○ - 60」になるはずだし、これが▲=22の根拠にはならない。>>70
ピタゴラスの定理の図形的解法から３辺の関係は推測できる…辺りから
「整数値なんだろ？」って適当な数字を入れて解いちゃいそうだなぁ（笑>>55
이런 문제를 내는 레벨 낮은 고등학교는 한국에도 있어.>>7
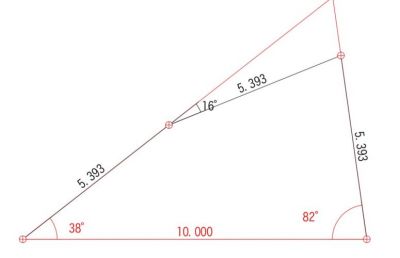
これやろｗこれ己と82℃に補助線入れると正三角形できるけど、それやると己ロ￢が120度になるんだが、、
￢の角度が60℃でロが120℃ってありえないし答えなんなの？
俺があほなの？>>100だけど俺がアホだったわ
전혀 모르겠다. 내가 어렸을 때에도, 도형 문제는 정말 싫었어.
既に >19 で書いたが。
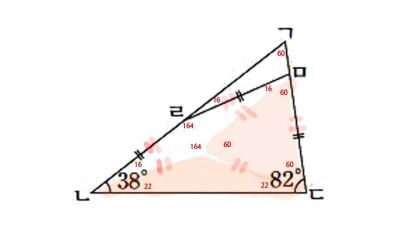
これ、設問間違い。図の中に2等辺三角形（22+22+136）と正三角形を描けば良いだけだったと考えたが。
38=22+16
82=60+22
16+16+164+164=360
180-164=16
算数は不得意である。解の形はㅁが垂直になる。
己ロLコみたいな記号で草
>>105
小４まで習った知識では解けない。>>108
日本風に書くと
イ ロ ハ>>110
＞内角の和が180度を使わなくても解けるんじゃないかな。
内角の和を使った回答を書いてみて。>>115
日本なら中学生までリミッター解除してQEDですね。分からなかったんでCADで書いてみた
초등학교 4학년 수학문제라는데 도와주십시오
117
ツイートLINEお気に入り108
8
レス投稿
画像をタップで並べ替え / 『×』で選択解除